一、加載Excel數據分析宏程序

Excel作為Office電子表格文件處理工具，不僅具有進行相關電子表格處理的功能，而且還帶有一個可以用來進行統計數據處理分析的宏程序庫——“分析工具庫”。通常計算機安裝了Office后，如果Excel電子表格“工具”項的下拉菜單中沒有“數據分析”命令，Excel并不能直接用來進行統計數據的處理分析，需要通過加載宏，啟動“數據分析”宏“分析工具庫”系統后才能運行統計數據的處理分析工具。

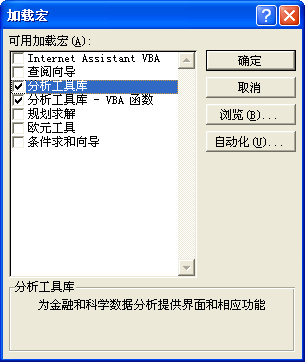
加載 “數據分析”宏，可點擊Excel中“工具”菜單，在彈出的“加載宏”對話框中選中“分析工具庫”及“分析工具庫-VBA函數”（如圖1所示）然后點擊“確定”。數據分析宏程序加載后，會在Excel的“工具”菜單里出現“數據分析”的命令選項。

完成了Excel“數據分析”程序宏的加載后，點擊工具菜單中的“數據分析”命令，即會彈出Excel的“數據分析”對話框（如圖2所示）。在整個分析工具宏程序庫中設有各種數據處理分析的工具宏程序，包括用于進行描述統計分析的描述統計和直方圖等分析工具宏，也包括可以進行推斷統計分析的方差分析、相關和回歸分析、統計推斷和檢驗以及時間序列指數平滑法等分析工具宏。

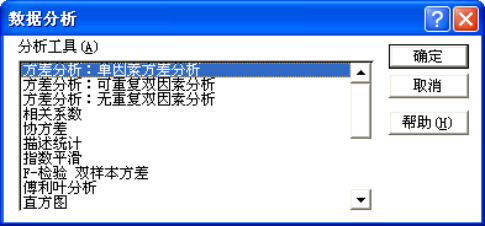
圖2　“數據分析”對話框

運行Excel“數據分析”宏中某一分析功能，并根據分析工具對數據進行分析，Excel的數據分析結果通常以統計表格或統計圖的形式直觀地顯示出來。

二、Excel的統計函數

Excel具有大量的內置函數，例如，財務函數、日期和時間函數、數學和三角函數以及統計函數等，共有300多個內置函數。內置函數就是預定義的內置公式，它使用參數并按照特定的順序進行計算。函數的參數是函數進行計算所必需的初始值。用戶把參數傳遞給函數，函數按特定指令對參數進行計算，把計算的結果返回給使用者。函數的參數可以是數字、文本、邏輯值或者單元格的引用，也可以是常量公式或其他函數。每個函數都有它需要的參數類型。在Excel提供的函數中，有77個統計函數（見表1）。

表1　Excel中統計函數及其功能

在Excel運行過程中調用統計函數主要采用兩種方法。第一種是在工作簿的單元格中直接輸入等號及統計函數的函數名稱，然后在有關的參數選項種填入正確的參數，即可得到計算結果。第二種是利用粘貼函數按鈕調用，單擊粘貼函數快捷按鈕，或點擊插入菜單中的函數（如圖3所示），即會彈出一個Excel函數選擇表，選擇其中的“統計”選項，屏幕上會彈出一個統計函數的選擇表（如圖3和圖4所示），選定需要調用的統計函數名稱，同樣會彈出該函數的初始值輸入對話框，在有關選項內填入確定的參數就能得到函數的計算結果。

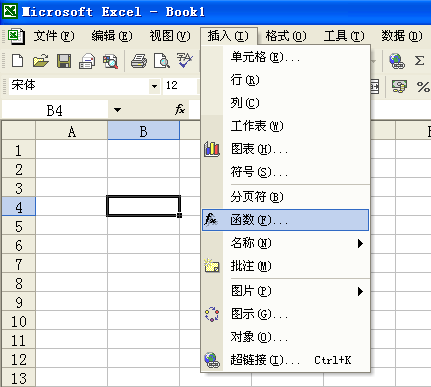
圖3　函數菜單選項　　　　　　　　　　　　

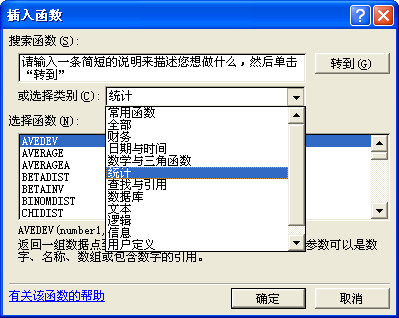
圖4　統計函數的選擇表

三、Excel在數據整理中的應用

（一）應用Excel進行統計分組

整理統計數據的重要方法是進行統計分組，顯示頻數分布形態。在Excel中有一個專用于統計分組的函數FREQUENCY，能進行統計分組，計算各組的頻數和頻率。下面以第二章中為例分別說明二者的操作方法。

首先，輸入待分組統計資料，如表2所示。

表2　某生產車間50名工人日加工零件數（單位：件 ）

對上表資料進行分組，操作步驟如下：

第一步，點擊K1單元格，從“插入”菜單中選擇“函數”項，或者單擊工具欄按鈕fx，屏幕彈出“插入函數”對話框，在“選擇類別（C）”欄中選擇“統計類”，如圖4所示；

第二步，在“選擇函數（N）”列表中選擇“FREQUENCY”，如圖5所示；

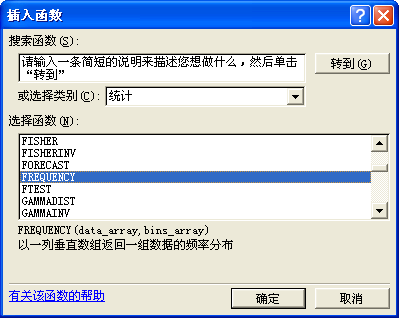
圖5　函數選項

第三步，單擊“確定”按鈕，彈出“函數參數”對話框，如圖6所示。首先，在對話框“Data_array”欄中輸入待分組計算頻數分布的原數據，本例中為“A1：J5”。然后，在“Bins_array”欄中輸入分組標志（按組距上限分組），本例可輸入“{109;114;119;124;129;134}”。在輸入過程中，數據前后必須加大括號，數據間用分號分割。輸入完后，單擊確定，這時在K1中顯示3，由于事先確定分為6組，選定“K1：K6”單元格作為放置計算結果的區域，按F2鍵，再按“Shift+Ctrl+Enter”組合健，即可顯示頻數分布結果，如圖7所示。

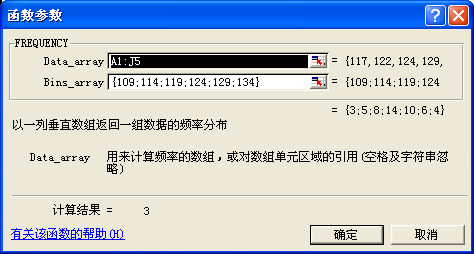
圖6　函數參數對話框                       

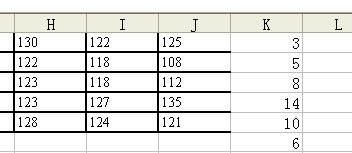
 圖7　計算結果

（二）應用Excel編制變量數列

1．單項數列的編制

下面以表3為例，說明其操作方法。

表3　單項式數列

首先，在A1單元格輸入“日產量”12、10、13、11、14、12、11、12、13、12，并將這10個數據輸入A2～A11中，然后選定數據所在的列A，單擊“數據”菜單的“排序”項，打開排序對話框，單擊確定，進行排序。排序之后，單擊“數據”菜單中的“分類匯總”，打開“分類匯總”對話框，如圖8所示，在“匯總方式”欄內選擇“計數”，單擊“確定”即可。

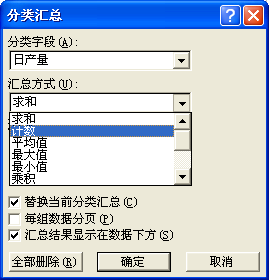
圖8　“分類匯總”對話框                            

 圖9　輸出結果

匯總之后，單擊左上邊數字“2”，可顯示單項式數列，如圖9所示

2．組距數列的編制

對于組距數列的編制，可以使用頻數函數Frequency進行統計。取得頻數分布后，可再列表計算頻數以及累計頻數和頻率。例如，對圖7的結果，編輯整理后可得組距式數列結果，如圖10所示。

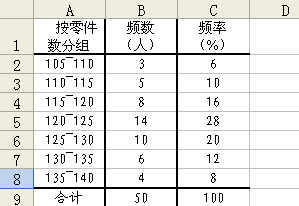
圖10　組距式數列結果

（三）應用Excel描述集中趨勢

描述集中趨勢的統計參數有均值、眾數、中位數等。在Excel中，對于未分組的資料可以用統計函數計算，對于已分組資料則根據公式計算。

1．算術均值

（1）簡單平均法

例如，某生產組5名工人生產同一種產品的日產量分別為60、70、80、90、100（單位：件），則計算方法為：

首先，將這5名工人的日產量輸入A1～A5單元格內，然后，利用AVERAGE函數計算均值，可單擊任一空單元格，輸入“=AVERAGE（A1：A5）”，回車確定，即得到日平均產量80（件／人）。

（2）加權平均法

利用分組數據可以直接計算加權均值。先列出計算表，然后用公式計算。

首先將分組資料輸入，例如A、B兩列，如圖11所示。

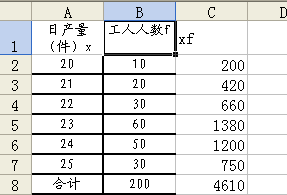
圖11　數據輸入視圖

計算C欄各組數值，單擊C2單元格，輸入“=A2*B2”，回車確定后即得出第一組數值。然后，利用填充柄功能，即鼠標指向C2單元格右下方小黑方塊，當鼠標指針變為黑十字時，按下鼠標左鍵，并向下拖拽至C7單元格后放開，得出C欄各組數值。然后單擊C8單元格并輸入“=SUM（C2：C7）”計算出C欄合計數，利用填充柄功能計算出B欄合計數。最后單擊任一空單元格，輸入“=C8/B8”，確定后得出工人平均日包裝量為23.05件。

（四）應用Excel描述離散趨勢

1．標準差

Excel提供了一組求標準差的函數，其中函數STDEVP是一個求標準差的函數；函數STDEVPA是求包含邏輯值和數字串數列的標準差的函數。這兩個函數操作方法類似，現以圖12為例說明標準差的計算方法。

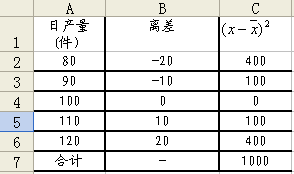
圖12　計算標準差

單擊任一單元格輸入“=STDEVP（A2:A6）”，按“確定”即得到標準差14.14件。

可以也通過函數對話框計算標準差。單擊“插入”菜單中的“函數”命令，在彈出的對話框中選擇“統計”類別里的STDEVP函數，打開STDEVP函數的對話框，在Numberl中輸入數據所在的區域“A2：A6”，確定后即可求得標準差。

2．加權式標準差

下面以圖13為例，說明其計算方法。

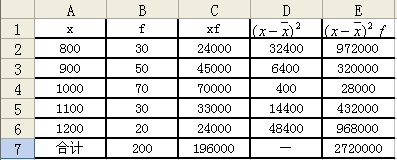
圖13　加權計算標準差

將資料輸入A、B兩列后，首先計算均值。單擊C2，輸入“=A2*B2”，得出24 000，利用填充柄功能，計算出C2~C6，然后單擊C7，輸入“=SUM（C2：C6）”，計算出合計數196 000，利用填充柄功能，計算出工人數合計200，再單擊任一空單元格，輸入“=C5／B7”，得出均值為980；接著計算離差平方及離差平方和。單擊D2單元格輸入“=（C2－980）^2”，確定后利用填充柄功能計算D數列數值；單擊E2單元格，輸入“=D2*B2”，計算加權離差平方，利用填充柄功能計算E列；單擊E7單元格，輸入“=SUM（E2：E6）”，計算離差平方和；最后，單擊任一空單元格，輸入“=SQR（E7／B7）”，即得總體標準差116.62。

四、Excel在抽樣估計中的應用

利用Excel提供的有關統計函數，可以對總體平均數進行區間估計。設從200名工人中隨機抽取20名工人調查其日產量，參閱案例1操作方法，計算出樣本平均數40件和樣本標準差7.5，要求在95％的概率保證程度下，估計該企業工人的平均日產量。

在A1、A2、A3單元格中分別輸入樣本容量、樣本均值、樣本標準差，即20、40、7.5。單擊A4，計算樣本平均誤差，輸入“=A3／SQRT（A1）”。利用函數NORMINV計算平均日產量的上限和下限。下面使用函數對話框方式使用函數。單擊A5單元格，選擇“插入”菜單中“函數”命令，打開“選擇函數”對話框，在“選擇類別”中選擇“統計”類別，在“選擇函數”欄內選擇“NORMINV”函數，單擊“確定”，打開NORMINV函數設置對話框，如圖14所示。

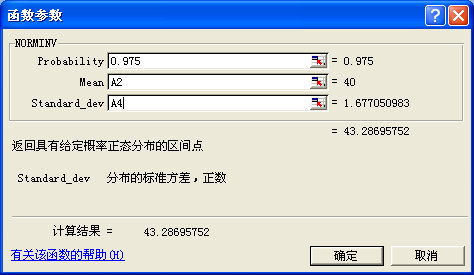
圖14　抽樣估計

本例中，給定的概率保證程度為95％，因此在進行NORMINV函數參數設置時，Probability項要輸入“0.95＋（1－0.95）/2”即0.975；在Mean和Standard_dev項內輸入樣本平均數A2、樣本平均誤差A4，確定后計算出樣本平均數的上限為43.29件。

在Probability項中輸入“（1－0．95）／2”即0.025，計算出樣本平均數的下限為36.71件，如圖15所示。

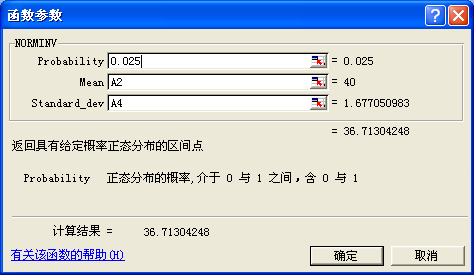
圖15　計算結果

五、Excel在指數分析中的應用

（一）綜合法總指數

本案例以表6中的數據資料為例。

表6　某企業產量和出廠價格

首先，將數據輸入Excel后，見圖16中A、B、C、D、E、F列。

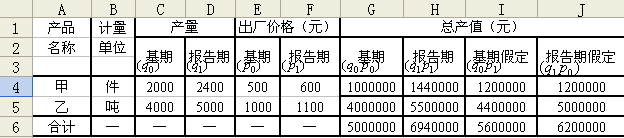
圖16　數據輸入方式

計算G、H、I、J四列的銷售額。對于G列，單擊G4單元格，輸入“=C4*E4”，并利用填充柄功能計算G5；H、I、J列均可仿此計算；之后單擊G6單元格，輸入“=SUM（G4：G5）”，并利用填充柄功能，計算出G、H、I、J各列的總產值。

1．數量指標綜合法指數的計算

數量指標綜合法指數，是以價格為同度量因素（權數）編制的商品銷售量指數，用來反映總產值的變動情況。在一般情況下，同度量因素（價格）要固定在基期。因此，單擊任一空單元格，輸入“=J6／G6*100”得124（％），即產量綜合法指數Kq=124％，它表明兩種商品的總產量綜合指數比基期上升24％（124％－100％），由于產量上升使總產值增加（J6－G6）為120萬元。

2．質量指標綜合法指數的計算

質量指標綜合法指數，是以銷售量為同度量因素（權數）編制的商品價格指數，用來反映價格的變動情況。在一般情況下，同度量因素（銷售量）要固定在報告期。因此，單擊任一空單元格，輸入“=H6／J6*100”，得111.9％，即價格綜合法指數kp=111.9％，它表明三種商品綜合價格指數報告期比基期上升了11.9％，由于價格上漲使總產值上升了（H6－J6）74萬元。

（二）平均法總指數

1．算術平均法總指數的計算

在一定條件下，根據基期同度量因素編制的數量指標綜合法總指數可以變形為加權算術平均法總指數。一般來說，加權算術平均法總指數多用于計算數量指標綜合法總指數。現以表7為例。

表7　產量個體指數和基期總產值

將數據輸入Excel后，見圖17中A、B、C列。

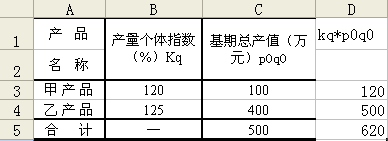
圖17　數據輸入方式

首先，計算D列數字：單擊D3單元格，輸入“=B3*C3”并利用填充柄功能計算D4；最后計算合計數，單擊D5輸入“=SUM（D3 : D4）”求出基期總銷售額，并利用填充柄功能計算C5。單擊任一空單元格，輸入“=D5／C5”，即得產量加權算術平均法總指數124％。

2．調和平均法總指數的計算

在一定條件下，根據報告期同度量因素編制的質量指標綜合法總指數可以變形為加權調和平均法總指數。一般來說，加權調和平均法總指數多用于計算質量指標綜合法總指數。現以表8為例。

表8　出廠價格個體指數和報告期總產值

將數據輸入Excel后，見圖18中A、B、C列。

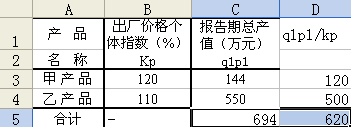
圖18　數據輸入方式

首先，計算D兩列數字，單擊D3單元格，輸入“=C3/B3*100”，然后利用填充柄功能計算D4的值；然后計算C5，輸入“=SUM（C3 : C4）”，并利用填充柄功能計算D5；最后單擊任一空單元格，輸入“=C5/D5”，即得到調和加權平均法價格總指數111.9%。

六、Excel在長期趨勢分析中的應用

（一）移動平均法

在Excel中，移動平均法可使用AVERAGE函數，利用填充柄功能求得，如圖19所示。

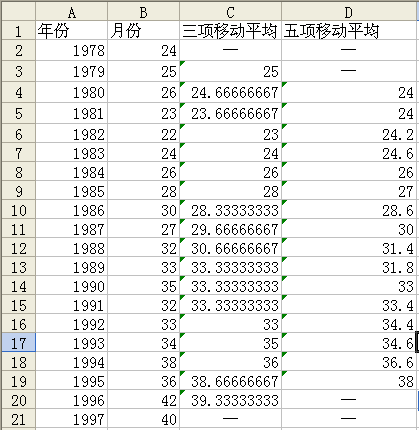
圖19　移動平均法計算

進行三項移動平均：可單擊C3單元格，輸入“=AVERACE（B2:B4）”，然后利用填充柄功能，計算C4~C20單元格的值。

進行五項移動平均：可單擊D4單元格，輸入“=AVERAGE（B2:B6）”，然后利用填充柄功能，計算D5~D19單元格的值。

（二）最小平方法

以圖20說明如何運用最小平方法來建立直線趨勢方程。

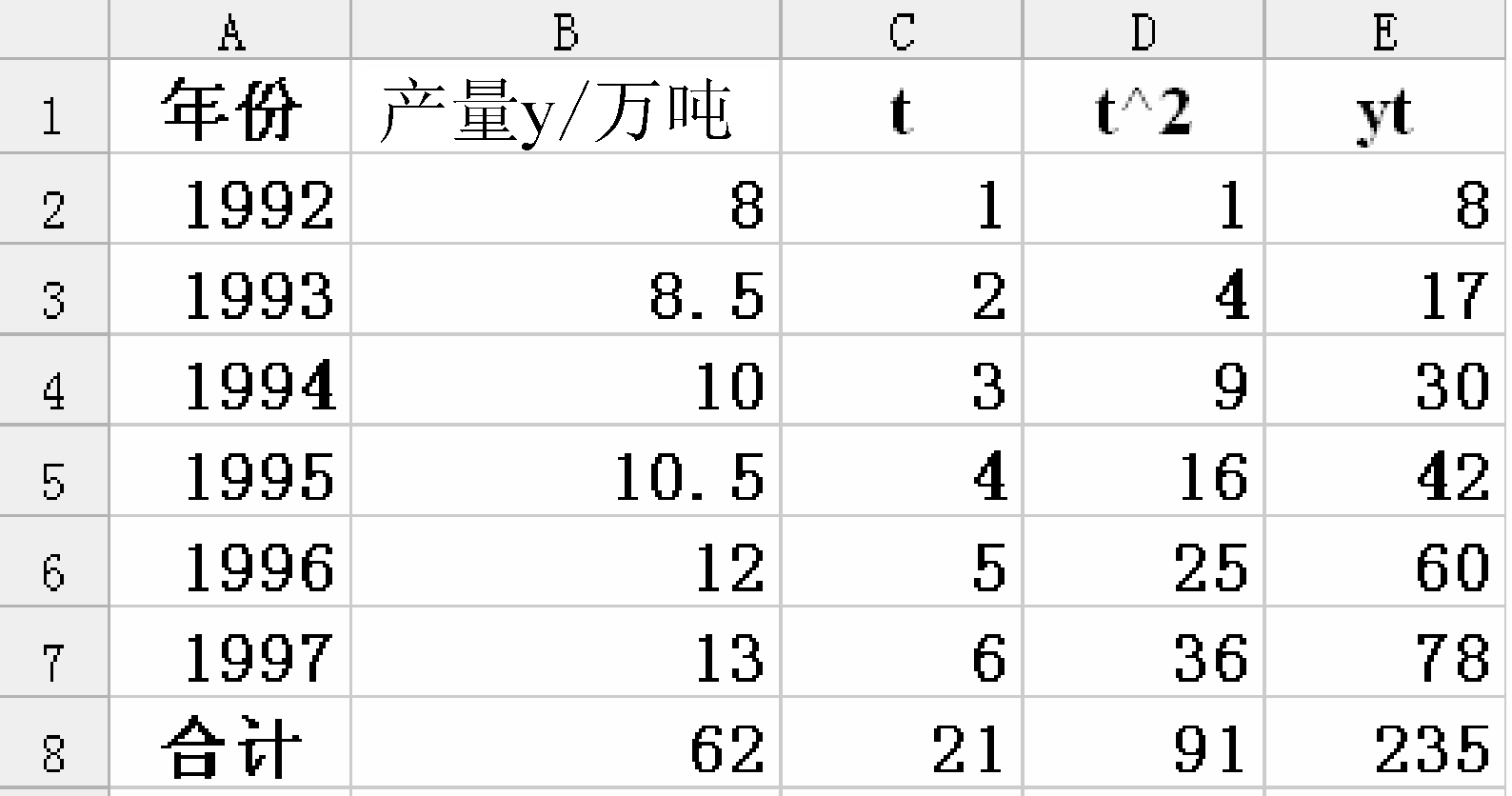
圖20　最小平方法

輸入A、B、C后，計算D列。單擊D2，輸入“=B2^2”，并用填充柄功能，計算D3～D7，再計算E列，單擊E2，輸入“=B2*C2”，并用填充柄功能，計算E3～E7。然后計算合計，單擊B8，輸入“=SUM（B2：B7）”得62，再并用填充柄功能，計算C、D、E各列的合計數。

下面計算參數a、b值，先計算b，單擊任一單元格，輸入“=（6*E8－B8*C8）/（6*D8－C8^2）”，確定后即得b的值1.028。再計算a，單擊任一單元格，輸入“=B8／6－1.028*C8／6”得a的值6.733。于是，建立直線趨勢方程，即yt=6.733+1.028t。

將C列t值依次代入直線趨勢方程yt=6.733+1.028t中，便得到y的預測值。

七、Excel在相關與回歸分析中的應用

（一）相關系數的計算

利用Excel計算相關系數，可以使用CORREL函數計算。利用圖21中的資料計算x與y相關系數。

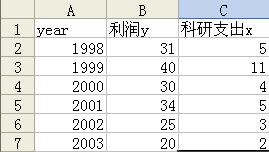
圖21　數據輸入

單擊“插入”菜單里的“函數”命令，選擇函數類別“統計”里的“CORREL函數”，打開相關系數函數CORREL對話框，如圖22所示。

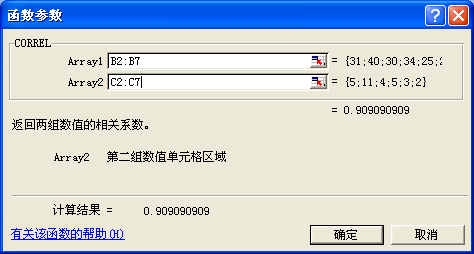
圖22　相關分析函數對話框

在Array1、Array2里分別輸入兩列數據所在區域“B2:B7”和“C2:C7”，即得相關系數0.909。

（二）一元線性回歸分析

利用“數據分析”宏中回歸分析，可以直接計算y對x的回歸模型。利用圖21中的資料計算y對x的回歸模型。

單擊“工具”菜單中的“數據分析”選項，彈出“數據分析”對話框，如圖23所示。

圖23　回歸分析選項

選中回歸選項，單擊“確定”按鈕。屏幕上將彈出“回歸”對話框，如圖24所示。

在“Y值輸入區域（Y）”中，輸入“B2:B7”，“X值輸入區域（X）”中輸入“C2:C7”，輸出選項如果默認，則輸出結果將在新工作表中顯示，單擊確定按鈕，EXCEL將自動生成一新工作表，表中顯示回歸分析結果，如圖25所示。從計算結果可見，回歸模型為。

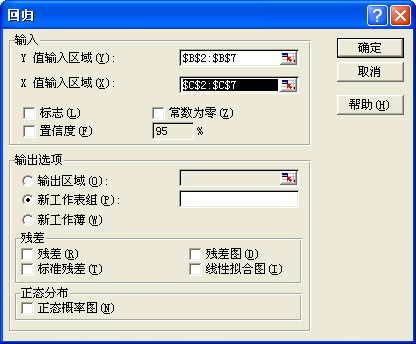
圖24　回歸分析對話框

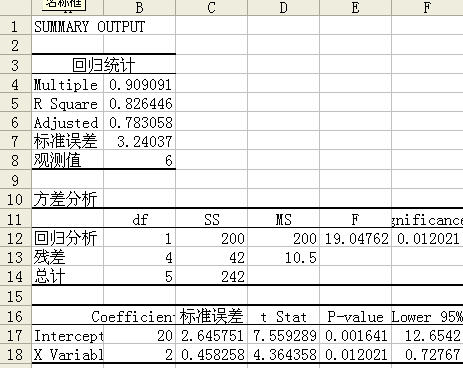
圖25　計算結果